КИНЕТИЧЕСКАЯ ТЕОРИЯ

КИНЕТИЧЕСКАЯ ТЕОРИЯ (от греч. kinesis—движение), основана на представлении о веществе как совокупности молекул, связанных молекулярными силами и находящихся в непрерывном движении.Наиболее простым случаем является случай газа, который согласно К. т. в первом приближении представляют себе состоящим из совершенно свободных, не связанных внутренними силами точечных молекул, хаотически носящихся с большой скоростью во всех возможных направлениях и пристолкновениях взаимодействующих по законам удара упругих тел. Из этих простых предпосылок без труда могут быть получены все основные свойства газов. Наиболее характерной особенностью газа является его способность беспредельно расширяться: газы практически мгновенно занимают любой объем, к-рый им предоставляется. Отсюда вытекает дальнейшее свойство газов—давление, к-рое они оказывают на стенки заключающих их сосудов. Сточки зрения К. т. это давление есть результат той «бомбардировки», к-рой подвергаются стенки сосуда со стороны непрерывно налетающих молекул газа. Из этого представления прямо вытекает основной закон газового состояния—закон Бойля-Мариотта. Действительно, уменьшая объем газа вдвое или втрое, мы заставляем летающие молекулы соответственно вдвое или втрое чаще ударяться о стенки сосуда, а следовательно давление должно возрасти вдвое или втрое. Этим качественным рассуждениям легко можно придать количественную форму и получить основную формулу К. т. газов. Подсчитаем для этого величину давления р, обусловленного ударами молекул. Ясно, что это давление должно быть пропорционально количеству ударов, испытываемых 1 см² стенки, и интенсивности толчка, сообщаемого каждым ударом. Количество ударов очевидно в свою очередь пропорционально числу молекул в 1 ель³ газа (N) и скорости этих молекул (v). Интенсивность же толчка, сообщаемого каждой молекулой, или импульс, как известно из механики, пропорциональна количеству движения молекулы, т. е. произведению ее массы на скорость—mv. Итак мы видим, что давление р пропорционально 2iv.mv=Nmv². В этой формуле нехватает только постоянного числового множителя, к-рый, как показывает простое вычисление, равен ¹/₃. Итак, p = ¹/₃Nmv². (1) При помощи этой простой формулы прежде всего можно определить скорость газовых молекул. Действительно N (число молекул в 1 см³) х m (масса молекулы)=плотности газа д; отсюдар =¹/₃ev²- Т. о. для вычисления скоростей молекул необходимо знание лишь плотностей. Такие вычисления дают напр. след. значения v. Кислород Азот Водород Углекислота 425 492 1.844 392 м/сек. Эти величины много превосходят скорость ветра при самых грозных ураганах и приближаются к скорости снарядов из орудий. Если эта молекулярная бомбардировка и не производит разрушающего действия, то только потому, что удары направлены совершенно хаотически во все стороны и в среднем друг друга уравновешивают. Пусть газ занимает объем У; по основной формуле давление, оказываемое этим газом, будет р = ¹{_sqv^s; но q = плотность = м объем ; если число молекул в объеме V будет N¹, а масса каждой—т, то М=Шт, а е= mm „ = -у- . Подставляя это значение для плотностей в основную формулу, получим Vs-v^-f², или 1 р • V - \ Wmv* - ²/₃№ • ("^) • С другой стороны основной закон газового состояния—закон Бойля-Мариотта-Гей-Люссака (см. Газы) гласит: pV— ВТ, где Т— абсолютная t°. Сравнивая это выражение с только-что полученной формулой, находим: рУ-у₃№(^)=ВТ. (2) Но ^- есть кинетическая энергия отдельной молекулы, а В—-постоянная величина. Т. о. из формулы (2) следует, что кинетическая энергия молекул пропорциональна абсолютной t° газа. Мы видим, что К. т. придает понятию t^D совершенно конкретный <s»8 физ. смысл: это есть не что иное, как энергия движения молекул газа; не существует «горячих» и «холодных» молекул, есть только молекулы, движущиеся с большей или меньшей скоростью. До сих пор предполагалось, что все молекулы движутся с одной и той же скоростью, которая обозначена буквой v. Простые соображения показывают, что это неверно. В самом деле, если бы даже в нек-рый момент все молекулы имели одинаковую по величине скорость, то уже в следующий момент вследствие столкновений, происходящих под самыми разнообразными углами, молекулы приобрели бы различную скорость. Выше мы видели, что скорость для молекул азота— главной составной части воздуха—при 0° равна приблизительно 500 ж/сек. Если бы такая молекула полетела вертикально вверх, то она бы могла подняться на высоту всего 12,Ъ км. Т. о. если бы все молекулы двигались с одинаковой скоростью, то максимальная высота, до к-рой могли бы подниматься вверх молекулы воздуха, т. е. теоретический предел атмосферы, был бы равен той же величине 12,5 км. На самом деле известно, что наиболее высокие северные сияния происходят еще на высоте 500 км, метеориты загораются на высоте 200 мит.д, Причина противоречия именно в том, что отождествляют среднюю скорость v с истинной скоростью. В действительности же встречаются молекулы как с меньшими, так и со значительно большими скоростями. Максвелл (Maxwell) впервые ввел в К. т. «закон распределения молекулярных скоростей», т. е. формулу, позволяющую вычислить, какая именно доля из всего числа молекул обладает заданной скоростью. По Максвеллу, состояние газа можно охарактеризовать как полный хаос; молекулы обладают всевозможными скоростями; чаще всего встречаются молекулы с нек-рой скоростью, к-рая является наивероятнейшей, но определенный процент молекул обладает гораздо большими и определенный процент—гораздо меньшими скоростями. Т. к. число молекул огромно и микроскоп, состояние газа характеризуется как полный хаос, то с тем ббль-шим правом для построения К. т. газов мбж-но воспользоваться методами статистики, методами теории вероятностей. Знаменитая формула распределения Максвелла, графически иллюстрируемая рисунком, имеет именно такой статистич. характер. Совершенно аналогичному закону подчиняется распределение всех случайных явлений вообще, например распределение случайных погрешностей наблюдения и т. п. (см. Вариационная статистика). Наиболее вероятное значение скорости газовых молекул, т. е. та скорость, которой обладает наибольшее число молекул газа, по сказанному ранее измеряется многими сотнями метров в секунду. Несмотря на это, молекулы перемещаются поступательно сравнительно медленно: в этом убеждает нас хотя бы относительная медленность распространения запахов. Причина кажущегося противоречия в том, что вследствие огромного числа молекул каждая из них непрерывно сталкивается с окружающими и по- тому постоянно меняет направление своего пути. Пространство, проходимое молекулой между двумя соударениями,—т. н. средняя длина свободного пути—имеет поэтому ничтожную величину. Эта средняя длина пути играет выдающуюся роль в целом ряде явлений, происходящих в газах. Таковы: 1. Диффузия (см.); если привести в соприкосновение два газа, то, как известно, тотчас Z.1 2,0 " " £ \ при Т=0°С tn l.i 1,в «? „ ^Ч <и ■ч о 3; 1,0 0,0 0.я и *■ " 0,4 0,э 0,2 - / О.' " 0 100 г00 300 400 S00 90.0 700 800 000 1000 1100 — скорость в ^м/сек. же начинается взаимное проникновение газов, обусловленное движением молекул— диффузия. Ясно, что чем больше средняя длина свободного пробега, тем больше и скорость диффузии. 2. Теплопроводность. В покоящемся газе, при отсутствии всяких потоков теплота передается, хотя и крайне медленно, путем теплопроводности. С точки зрения К. т. это надо понимать так, что молекулы более нагретой части газа путем постоянных соударений передают свой избыток количества движения остальным молекулам. Но можно то же явление трактовать и как диффузию молекулы из более нагретой части газа в более холодную и наоборот. 3. Внутреннее трение. Когда один слой газа скользит вдоль другого, то молекулы диффундируют через поверхность раздела обоих слоев; при этом молекулы, диффундирующие из неподвижного или более медленно движущегося слоя, слегка замедляют движение более быстрого слоя, и обратно—молекулы, попадающие из скользящего слоя в неподвижный, стремятся привести в движение последний. Вследствие этого скользящий слой испытывает совершенно такое же трение, как твердое тело, движущееся по шероховатой поверхности. Т. о. все эти три явления тесно связаны со средней длиной свободного пробега; все они позволяют эту длину вычислить. Однако в виду математических трудностей вычисление может быть выполнено лишь при условии, если считать, что молекулы взаимодействуют, как гладкие бильярдные шары. Т. к. это условие страдает чрезмерной упрощенностью, то и результаты не отличаются особенной точностью. Однако порядок величины во всех случаях получается правильный. Для наиболее известных газов при нормальном давлении (760 мм Hg) средняя длина свободного пути имеет следующие значения в миллионах долях см: Водород Кислород Азот Углекислота Хлор 18,3 9,95 9,44 6,29 4,57Х 10-е _См. Если сопоставить величину среднего пути молекулы 0₂ с ее скоростью, то легко подсчитать, что эта молекула должна испытывать приблизительно 4.500 млн. соударений в секунду. В наст, время существует целый ряд методов, позволяющих находить число молекул в 1 см³ газа. Не останавливаясь на их изложении, упомянем только один из них. Голубой цвет неба, как известно, обусловлен рассеянием солнечного света молекулами воздуха. По Релею, интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны (чем и объясняется тот факт, что рассеянный свет содержит наибольшее количество лучей короткой длины волны т. е. синих и голубых) и прямо пропорциональна L—числу молекул в одном см³. Т. о. из наблюдений над интенсивностью голубого цвета неба можно вычислить L. Этот и другие методы согласно дают для L (т. н. Лош-мидтово число) величину около 27х10¹⁸, число же молекул в грамм-молекуле (постоянная Авогадро) равно 60,64 х10²². Последним числом при работах пользоваться удобнее, т. к. оно не зависит от давления и одинаково для вещества в твердом, жидком и газообразном состояниях. Об огромности этих чисел трудно составить наглядное представление. Достаточно сказать, что наилучший достижимый современными техническими средствами «вакуум» (пустота рентгеновской трубки Кулиджа) все еще содержит 27 млрд. молекул в 1 см³.—Зная среднюю длину пути и число молекул в единице объема, можно вычислить и размеры молекул. Такие вычисления дают напр. для диаметра молекул следующие числа: Кислород Азот Водород 2,9 3,1 2,3 X 10-« СИ. Большие органические молекулы, напр. молекулы белков, имеют гораздо бблыние размеры; однако мельчайшие бацилы содержат все еще 10^е—-10' молекул, красный кровяной шарик—10⁹, а сперматозоиды человека—10⁸молекул.—-Все изложенное до сих пор представляет только «первое приближение» к действительности. В самом деле при выводе основного уравнения мы предполагали, что молекулы—точки, не имеющие объема и не связанные друг с другом никакими силами взаимодействия; при выводе средней длины пути и числа соударений предполагалось, что молекулы—упругие шарики. Если учесть конечный объем молекул и наличие сил сцепления, к-рые могут быть обнаружены, хотя и в слабой степени, даже в газах, то простое уравнение состояния газа, выражаем, законом Бойля-Мариотта—Гей-Люссака:р v—RT .(см. Газы), заменяется более сложным уравнением Бан-дер-Ваальса (см.Газы, Ван-дер- Ваалъса закон, Жидкости): (р+—,-).(!>-Ь) = = RT, где член -" представляет поправку на молекулярные взаимодействия, а член Ъ— поправку на истинный объем молекул. За самое последнее время разработаны методы, позволяющие определять молекулярные ско- рости и среднюю длину пробега непосредственно, а не косвенно, путем вычисления, как это было изложено выше. При этом все полученные путем вычислений и приведенные выше числа, равно как и Максвелловский закон распределения молекулярных скоростей, нашли себе превосходное подтверждение. К. т. твердых тел разработана пока еще очень слабо, а К. т. жидкостей в сущности еще совсем не существует: настолько велики математические трудности, встречающиеся при перенесении К. т. газов на другие состояния. (См. также Броуновское движение.) Лит.: Бачинский А., Кинетическая теория газов, Москва, 1908; Блох Е., Кинетическая теория газов, М.—Л., 1925; Тимирязев А., Кинетическая теория материи, M.—П., 1923; Н е г shield К., Kinetische Theorie der Warme, Braunschweig, 1925. Э. Шпольсшш.

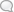Смотрите также:

КИНЕТИЧЕСКОЕ ОЩУЩЕНИЕ (кинестезия), двигательное чувство, способность определять направление и объем движений в различных суставах. К. о. относится к разряду глубокой чувствительности (проприо-цептивные импульсы от суставных концов костей, сухожилий и мышц) и входит ...
КИНЕТОПЛАСТ, морфологический комплекс, образуемый у трипаносом и близких им жгутиковых блефаропластом и параба-зальным тельцем и связанный со жгутом. Называется также кинетонуклеусом.хотя никакого отношения к ядру не имеет.
КИНО, Kino, сгущенный до сухого состояния сок дерева Pterocarpus marsupium Roxb., ceM.MOTbUibKOBbix(Papilionaceae-Dalbergieae), достигающего 25 м высоты. Дерево растет на Цейлоне и в Ост-Индии. К. имеет вид красно-бурых табличек, легко растворимых ...
КИНОПЛАЗМА, часть протоплазмы, так или иначе связанная с сокращением и соответственными движениями клетки или ее частей. Термин К. применяется Кольцовым для обозначения жидкой протоплазмы, входящей в состав сократительных элементов (мышечных ...
КИНУРЕНОВАЯ КИСЛОТА (у-оксихино-сн с(ОН) лин-/?-карбоноваяк-та), л\С/л C10H,NO3, кристаллы, псу >/ ...